• Персептрон
• Сигмоидальный нейрон
• Инстар Гроссберга
• Нейроны типа WTA
• Нейрон Хебба
• Радиальный нейрон

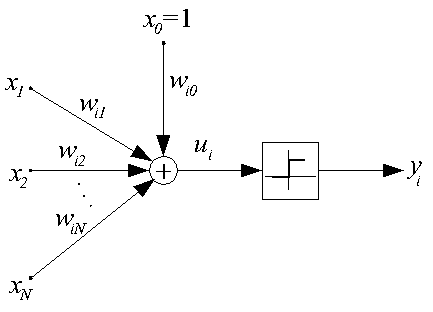
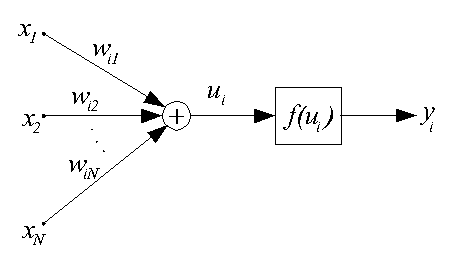
Данная модель искусственного нейрона (ИН) предложена в 1943 г. и называется также моделью МакКаллока-Пится. В этой модели нейрон считается бинарным элементом, его структурная схема представлена ниже.

Выходной сигнал нейрона может принимать только два значения {0, 1} по следующему правилу:

• y_i=f(u_i)=1, если u_i>=0;
• y_i=f(u_i)=0, если u_i<0.

Обучение персептрона требует учителя, т.е. множества {<X¹, d¹_i>, ..., <X^p, d^p_i>} пар <вектор входных сигналов X^k, ожидаемое значение выходного сигнала d^k_i>. Обучение (отыскание весовых коэффициентов w_ij) сводится к задаче минимизации целевой функции

К сожалению, для персептрона в силу разрывности функции f(u_i) для отыскания минимума E(W_i) применимы методы оптимизации только нулевого порядка.

На практике для обучения персептрона чаще всего используется правило персептрона, представляющее собой следующий простой алгоритм.

1. Выбираются (как правило, случайно) начальные значения весов w_ij (j=0, 1, 2, ..., N) нейрона.
2. Для каждой обучающей пары <X^k, d^k_i> выполняется ряд циклов (их номера обозначим через t) уточнения значений входных весов по формуле w_ij(t+1)=w_ij(t)+dw_ij(t), где
   • dw_ij(t)=0, если y_i(t)=d^k_i;
   • dw_ij(t)=x^k_j, если y_i(t)=0, а d^k_i=1;
   • dw_ij(t)=-x^k_j, если y_i(t)=1, а d^k_i=0.

Процесс обработки текущей обучающей пары завершается

• либо а) на цикле, в котором все dw_ij(t)=0,
• либо б) после достижения предельного количества циклов.
  

Следует отметить, что правило персептрона представляет собой частный случай предложенного много позже универсального правила обучения Видроу-Хоффа

Функционирование обученного персептрона в режиме классификации легко проиллюстрировать графически на примере двухвходового нейрона с поляризацией, структурная схема которого дана ниже.

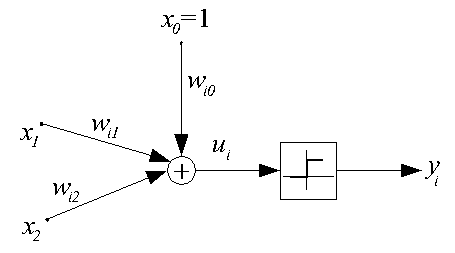
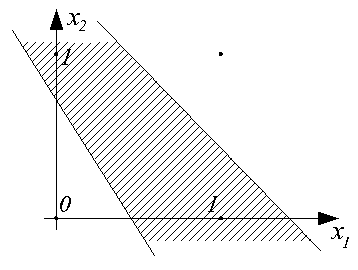
Для такого нейрона u_i=w_i0+w_i1x₁+w_i2x₂. Это выражение определяет плоскость в трехмерном пространстве <x₁, x₂, u_i>, эта плоскость пересекается с плоскостью <x₁, x₂> по линии, определяемой уравнением

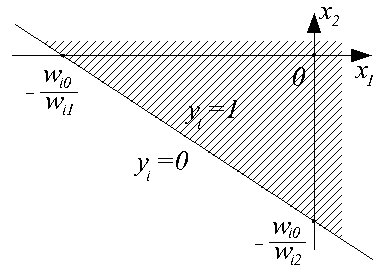
Эта линия разбивает пространство входных сигналов <x₁, x₂> на две области: в одной из них (заштрихованной) значения u_i>0, и, следовательно, функция активации принимает значение 1; в другой - u_i<0, и y_i=0.

Таким образом, наглядно видно, что персептрон является простейшим линейным классификатором. С его помощью можно обеспечить, например, классификацию, реализующую логические функции И и ИЛИ над входами x₁ и x₂, как это показано на рисунках.

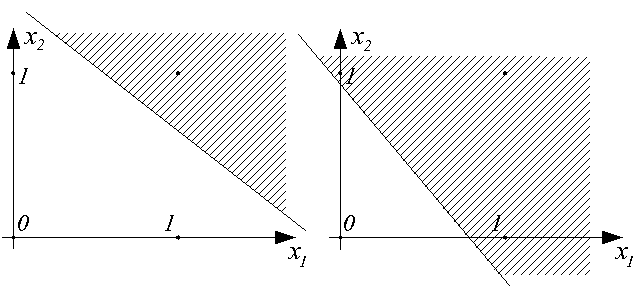
Однако реализовать логическую функцию "исключающее ИЛИ" уже невозможно (см. рисунок ниже).

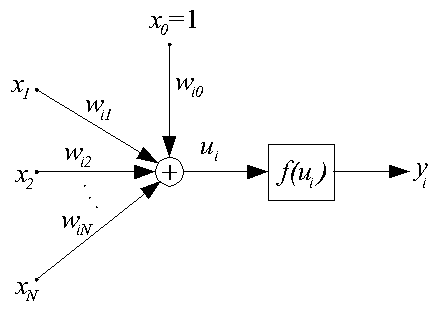
Нейрон данного типа устраняет основной недостаток персептрона - разрывность функции активации f(u_i). Структурная схема сигмоидального нейрона представлена ниже.

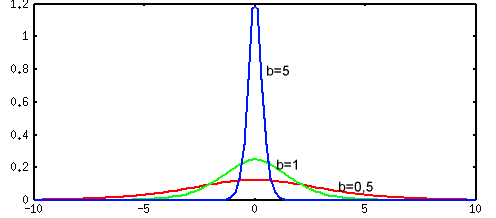
В качестве функции активации f(u_i) выступает сигмоидальная функция (т.е. функция, график которой похож на букву S). На практике используются как униполярные, так и биполярные функции активации.

Униполярная функция, как правило, представляется формулой

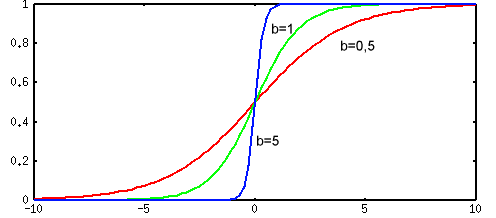
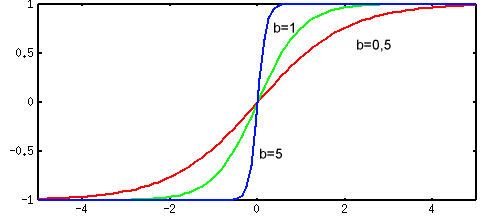
Коэффициент b определяет "крутизну" функций и выбирается пользователем (на практике b для упрощения назначают обычно равным 1).

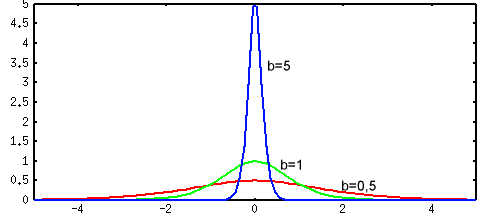
Производная униполярной функции активации имеет вид

Для обучения сигмоидального нейрона используется стратегия "с учителем", однако, в отличие от персептрона, для поиска минимума целевой функции

J-ая компонента вектора градиента имеет вид

Также возможно обучение сигмоидального нейрона и дискретным способом - сериями циклов уточнения входных весов для каждой эталонной пары <X^k, d^k_i> (см. правило персептрона). При этом коррекция весов после каждого цикла выполняется по следующей формуле:

Необходимо напомнить, что все методы поисковой оптимизации первого порядка - это методы локального поиска, не гарантирующие достижения глобального экстремума. В качестве попытки преодолеть этот недостаток было предложено обучение с моментом, в котором коррекция весов выполняется следующим образом:

Особенностями инстара, отличающими его от нейронов ранее рассмотренных типов, являются следующие:

1. функция активации f(u_i) часто линейна, т.е. y_i=u_i;
2. входной вектор X нормализован так, что его эвклидова норма равна 1;
3. обучение инстара возможно как с учителем, так и без него.

Нормализация элементов вектора X производится по следующей формуле:

Обучение инстара с учителем производится дискретно по правилу Гроссберга

На процесс обучения инстара решающее влияние оказывает величина коэффициента обучения nu. При nu=1 веса w_ij принимают значения соответствующих входов x^k_j текущей эталонной пары за один цикл обучения (при этом происходит абсолютное "забывание" предыдущих значений w_ij(t)). При nu<1 в результате обучения коэффициенты w_ij принимают некоторые "усредненные" значения обучающих векторов X^k, k=1, 2, ..., p.

Предположим, что i-ый инстар был обучен на единственной положительной эталонной паре <X¹, 1>. При этом вектор входных весов инстара W_i=[w_i1, w_{i2, ...,}w_iN]^T=X¹. В режиме классификации на вход инстара подается вектор X², тогда на выходе вырабатывается сигнал

Поскольку входные векторы X¹ и X² нормализованы (т.е. |X¹|₂=|X²|₂=1), то выходной сигнал инстара равен просто косинусу угла между векторами X¹ и X².

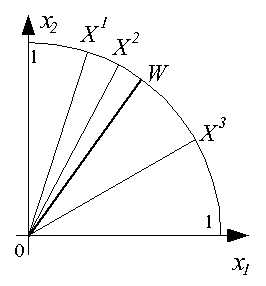
Функционирование инстара наглядно иллюстрируется графически. В режиме обучения при предъявлении, например, трех положительных примеров, содержащих двухкомпонентные векторы X¹, X² и X³, подбирается вектор входных весов W, представляющий собой "усреднение" этих входных векторов, как это показано ниже.

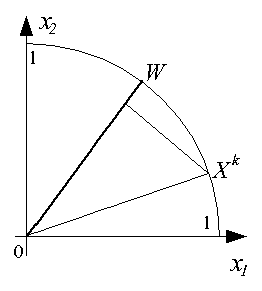
В режиме классификации при подаче на вход инстара очередного вектора X^k определяется степень его близости к "типичному" вектору W в виде косинуса угла между этими векторами, как это показано ниже.

Обучение инстара Гроссберга без учителя предполагает случайный выбор начальных значений входных весов w_ij и их нормализацию, подобную нормализации вектора входных сигналов X. Дальнейшее уточнение весов реализуется следующей формулой:

Нейроны типа WTA (Winner Takes All - победитель получает все) всегда используются группами, в которых конкурируют между собой. Структурная схема группы (слоя) нейронов типа WTA представлена ниже.

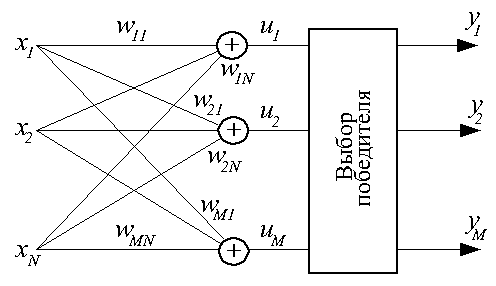
Каждый конкурирующий нейрон в группе получает одни и те же входные сигналы. Каждый нейрон рассчитывает выходной сигнал своего сумматора обычным образом u_i=sum[j=1:N](w_ij*x_j). По результатам сравнения всех u_i, i=1, 2, ..., M, выбирается нейрон-победитель, обладающий наибольшим значением u_i. Выходной сигнал y_i нейрона-победителя получает значение 1, выходные сигналы всех остальных нейронов - 0.

Для обучения нейронов типа WTA не требуется учитель, оно практически полностью аналогично обучению инстара Гроссберга. Начальные значения весовых коэффициентов всех нейронов выбираются случайным образом с последующей нормализацией относительно 1.
При предъявлении каждого обучающего вектора X^k определяется нейрон-победитель, что дает ему право уточнить свои весовые коэффициенты по упрощенному (в силу бинарности y_i) правилу Гроссберга

Понятно (см. инстар Гроссберга), что в каждом цикле обучения побеждает тот нейрон, чей текущий вектор входных весов W_i наиболее близок входному вектору X^k. При этом вектор W_i корректируется в сторону вектора X^k. Поэтому в ходе обучения каждая группа близких друг другу входных векторов (кластер) обслуживается отдельным нейроном.

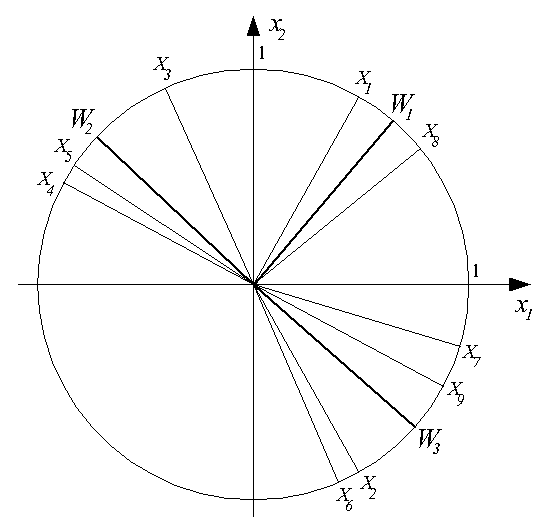
Рисунок ниже иллюстрирует результат обучения слоя нейронов типа WTA на последовательности девяти двухкомпонентных входных векторов X¹, X², ..., X⁹. Здесь были выделены три кластера входных векторов {X¹, X⁸}, {X³, X⁴, X⁵} и {X², X⁶, X⁷, X⁹}. За их распознавание отвечают три нейрона с векторами входных весов W₁, W₂ и W₃ соответственно.

Серьезная проблема в использовании нейронов типа WTA - возможность возникновения "мертвых" нейронов, т.е. нейронов, ни разу не победивших в конкурентной борьбе в ходе обучения и поэтому оставшихся в начальном состоянии. Для исключения "ложных" срабатываний в режиме классификации мертвые нейроны после окончания обучения должны быть удалены.

Для уменьшения количества мертвых нейронов (и, следовательно, повышения точности распознавания) используется модифицированное обучение, основанное на учете числа побед нейронов и шрафовании наиболее "зарвавшихся" среди них. Дисквалификация может быть реализована либо назначением порога числа побед, после которого слишком активный нейрон "засыпает" на заданное число циклов обучения, либо искусственным уменьшением величины u_i пропорционально числу побед.

Д.Хебб, исследуя поведение природных нервных клеток, зафиксировал (1949г.) усиление связи двух взаимодействующих клеток при их одновременном возбуждении. Это позволило ему предложить правило уточнения входных весов нейрона в следующем виде:

Особенностью правила Хебба является возможность достижения весом w_ij произвольно большого значения за счет многократного суммирования приращения в циклах обучения. Одним из способов стабилизации процесса обучения по Хеббу служит уменьшение уточняемого веса w_ij(t) на величину, пропорциональную коэффициенту забывания gamma. При этом правило Хебба принимает вид

К сожалению, при обучении по правилу Хебба нейрона с линейной функцией активации стабилизация не достигается даже при использовании забывания. В 1991г. Е.Ойя предложил модификацию правила Хебба, имеющую следующий вид :

Нейроны данного типа существенно отличаются от ранее рассмотренных. Они используются только группами, составляя первый слой в многослойных радиальных сетях. Структурная схема такого нейрона дана ниже.

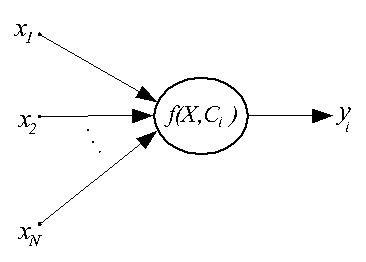
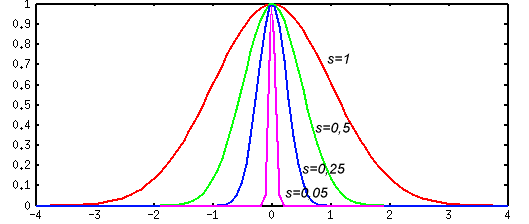
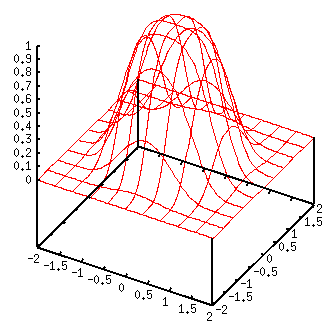
Принципиальное отличие радиального нейрона от сигмоидального (и персептрона) - в том, что сигмоидальный нейрон разбивает многомерное пространство входных сигналов гиперплоскостью, а радиальный - гиперсферой.

Обучение радиального нейрона заключается в подборе параметров радиальной функции C_i и s_i. Подробно алгоритм обучения радиальных сетей приведен в соответствующем разделе позже. Здесь же в качестве примера приведено выражение, часто используемое для корректировки положения центра нейрона после предъявления k-ого обучающего вектора